يشير الانحراف المعياري، المعروف أيضًا باسم SD أو المشار إليه بالرمز “σ”، إلى مدى انحراف القيمة عن القيمة المتوسطة. يشير الانحراف المعياري المنخفض إلى أن القيم غالبًا ما تكون ضمن بضعة انحرافات معيارية عن المتوسط. في المقابل، يشير الانحراف المعياري الكبير إلى أن القيم تتجاوز المتوسط. قبل حساب الانحراف المعياري، هناك العديد من الأشياء التي يجب معرفتها. يعد فهم الانحراف المعياري في إدارة المشاريع أمرًا بالغ الأهمية مثل أي عملية أخرى لتقييم تقلبات المشروع ومخاطره.
إن حساب الانحراف المعياري في برنامج Excel يعد مهمة صعبة للغاية نظرًا لوجود العديد من الأشياء التي يجب تذكرها. على سبيل المثال، هناك أنواع مختلفة من البيانات مجمعة أو غير مجمعة، كما تتغير صيغة الانحراف المعياري أيضًا. نظرًا لأن تعلم العديد من الأشياء المختلفة من مصادر مختلفة سيزيد من التعقيد، لتسهيل الموقف، إليك دليل يغطي أهم الموضوعات المتعلقة بالانحراف المعياري وكيف أن الانحراف المعياري مهم أيضًا لإدارة المشاريع.
احصل على دورة تدريبية في إدارة المشاريع (PMP) وتفوق في هذا المجال.
ما هو الانحراف المعياري؟
هل تبحث عن تعريف الانحراف المعياري؟ في الإحصاء الوصفي، يقيس الانحراف المعياري مدى انتشار أو تشتت مجموعات البيانات حول متوسطها. يعد الانحراف المعياري ذا أهمية خاصة في إدارة المشاريع، لأنه يساعد في تقييم تباين المشروع. يكشف الانحراف المعياري عن كيفية انحراف مقاييس المشروع عن المتوسط المتوقع، حيث تشير القيم الأعلى إلى تباين أكبر ومخاطر محتملة.
يكشف مقياس التباين في مجموعات البيانات عن المتوسط عن كيفية توزيع البيانات عبر البيانات المعطاة. يمثل الجذر التربيعي لتباين العينة الانحراف المعياري لمجتمع إحصائي أو متغير عشوائي أو مجموعة بيانات أو توزيع احتمالي.
يتم حساب الانحراف المتوسط لمتوسط الحساب على أنه x1، x2…xn إذا كان هناك n ملاحظة بقيم x1، x2…xn. ومع ذلك، فإن مجموع مربعات الانحرافات عن المتوسط لن يبدو مؤشرًا دقيقًا للتشتت. من المرجح أن تكون الملاحظات xi قريبة من المتوسط x إذا كان متوسط الاختلافات التربيعية عن المتوسط منخفضًا.
هذا التشتت موجود عند مستوى أقل. إذا كان هذا الإجمالي مرتفعًا، فهناك انحراف أكبر بين الملاحظات ومتوسط x. ونتيجة لذلك، نستنتج أن ∑(xi−x̄)2 هو مؤشر موثوق لمستوى التشتت أو التشتت.
يعد الانحراف المعياري من بين أهم مقاييس المخاطر التي يستخدمها الباحثون أو مديرو المحافظ أو المستشارون. يتم الكشف عن الانحراف المعياري لصناديق الاستثمار المشتركة، فضلاً عن المنتجات الأخرى، من قبل مجموعات الاستثمار. يكشف التشتت الكبير عن مدى انحراف عائد الاستثمار عن متوسط العائد المتوقع. غالبًا ما يتم تقديم هذه البيانات للمستثمرين والمستخدمين النهائيين نظرًا لسهولة فهمها.
لماذا الانحراف المعياري مهم؟
هناك العديد من الأسباب التي تجعل الانحراف المعياري مهمًا. فيما يلي بعض منها:
- كلما كانت البيانات متفرقة، أصبحت النتائج أسهل للفهم.
- سيكون الانحراف المعياري لتوزيع مجموعة البيانات أعلى بالفعل كلما كانت مجموعة البيانات موزعة بالتساوي.
- يستخدم قادة الشركات الانحراف المعياري في برنامج Excel للشؤون المالية لفهم إدارة التهديدات واتخاذ خيارات استثمارية أكثر حكمة.
- يسهل حساب هوامش الخطأ التي تظهر عادة في نتائج الاستطلاع.
ما مدى أهمية الانحراف المعياري لإدارة المشاريع؟
إن الانحراف المعياري لمدير المشروع في إدارة المشروع مهم جدًا لقياس تباين أداء المشروع. يسمح قياس عامل التباين لمدير المشروع بتحديد اتجاهات الاختلافات المحتملة في الجدول الزمني للمشروع والميزانية، وبالتالي يساعد بشكل أساسي في إدارة المخاطر وتخصيص الموارد المناسبة. على سبيل المثال، إذا كان الانحراف المعياري للمشروع منخفضًا، فإن مدة المهمة تقدم موثوقية عالية، بينما إذا كان الانحراف المعياري مرتفعًا، فإنه يحتاج إلى تحكم صارم في التباين.
الانحراف المعياري في امتحان شهادة PMP®
يضمن اختبار شهادة PMP® أن المتقدمين يفهمون أهمية الانحراف المعياري في إدارة مخاطر المشروع والجودة. من المؤكد أن إحدى المهارات التي سيتم اختبارها هي ما إذا كان المرشح قادرًا على حساب وتحليل الانحراف المعياري بشكل صحيح، مع مراعاة التطبيقات الصحيحة.
على سبيل المثال، سيتمكن مدير المشروع الذي يعرف الانحراف المعياري لجدول المشروع من اكتشاف وإدارة التأخيرات المحتملة في تنفيذ المشروع في الوقت المحدد. والفكرة الرئيسية حول معرفة المفهوم الأساسي فيما يتعلق بالانحراف المعياري لا تتلخص في اجتياز الاختبار فحسب، بل وأيضًا في إدارة المشاريع في الحياة الواقعية من أجل تنفيذها في الوقت المحدد وفي حدود الميزانية. وسيتمكن مدير المشروع الذي يفهم الانحراف المعياري من تقديم مشاريع ناجحة بشكل أفضل باستمرار.
تطبيقات الانحراف المعياري
يُستخدم الانحراف المعياري في الإحصاء في العديد من العمليات، وهو أحد الأسباب التي تجعل العديد من الجامعات والمجالس المدرسية تفضل هذا الموضوع في المنهج الدراسي بدلاً من أي شيء آخر. وفيما يلي بعض تطبيقات الانحراف المعياري.- يقوم المسوقون في كثير من الأحيان بحساب الانحراف المعياري للإيرادات المتولدة لكل إعلان لتحديد مقدار الانحراف المعياري والتباين في الأرباح المتوقع من إعلان معين.
- يقوم مديرو الموارد البشرية في كثير من الأحيان بتحديد الانحراف المعياري للأرباح في صناعة معينة، حتى يتمكنوا من تحديد نوع التباين في الراتب الذي يجب تقديمه للمجندين.
- لفهم مدى التنوع في أعمار الأشخاص، فإنهم يقدمون التأمين؛ ويقوم باحثو التأمين في كثير من الأحيان بتحديد الانحراف المعياري لذلك العمر.
- يمكن للمعلمين أو المدربين أو الأساتذة تحديد الفصول التي شهدت أكبر تنوع في نتائج الامتحانات بين الطلاب عن طريق حساب الانحراف المعياري لنتائج الامتحانات للفصول المختلفة.
هل تبحث عن معرفة المزيد عن إدارة المشاريع؟ ابدأ في تلقي دورات إدارة المشاريع عبر الإنترنت على الفور وتفوق في الدورة!
احصل على نظرة عميقة حول دورات إدارة المشاريع الرائجة في SPOTO:
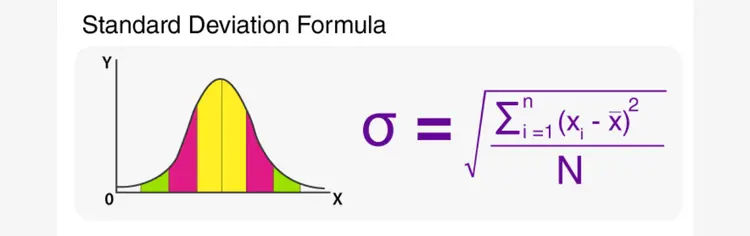
صيغة الانحراف المعياري (SD)
الانحراف المعياري هو أحد أكثر المواضيع شمولاً في الهندسة وحدها. واجه العديد من الطلاب الكثير من الصعوبات مع جميع جوانب الانحراف المعياري وحده. كما يتم استخدام الانحراف المعياري لاحقًا في العديد من الأشياء، مثل مقاييس التشتت، مما يجعله أكثر تعقيدًا. ولكن الحقيقة أن حساب الانحراف المعياري ليس بالأمر الصعب، حتى لو كان أسهل شيء يحسبه الشخص على الإطلاق. لا شك أن بعض المشكلات تستغرق ساعات من الحسابات، ولكن بصرف النظر عن ذلك، فإن كل شيء يعمل بشكل جيد.
الطريقة الأسهل لحساب الانحراف المعياري هي ببساطة حساب متوسط البيانات المقدمة. الآن فقط احسب التباين، وهو الخطوة قبل الأخيرة في حساب الانحراف المعياري. بعد ذلك، يتم وضع جميع القيم في الصيغة الموضحة أدناه. لذا، دعنا نفهم كيفية إيجاد صيغة الانحراف المعياري.
صيغة حساب الانحراف المعياري
من الناحية النظرية البسيطة، يمكن حساب الانحراف المعياري بسهولة من خلال الجذر التربيعي للتباين. لحساب التباين، يحتاج الشخص إلى حساب المتوسط أولاً. مع وضع ذلك في الاعتبار، إليك صيغة انحراف معياري نموذجية لحساب التباين المعياري. رمز الانحراف المعياري هو σ.- x̄ = متوسط نتيجة مجموعة البيانات
- xi = النقطة رقم ith في قيمة مجموعة البيانات
- n= حجم مجموعة البيانات من حيث نقاط البيانات
كيف يتم حساب الانحراف المعياري؟
خطوات حساب الانحراف المعياري
نظرًا لأن حساب المتوسط إلزامي ويُستخدم كثيرًا مع الانحراف المعياري للعينة، فإن العديد من الخبراء يفضلون حساب المتوسط أولاً أثناء حساب الانحراف المعياري. ومع ذلك، سيتغير هذا القرار نظرًا لاختلاف تفضيلات الأشخاص، إما لحساب المتوسط بشكل منفصل أو أثناء حساب الانحراف المعياري. لذا، نترك هذا القرار للقارئ. تحقق أدناه من كيفية إيجاد الانحراف المعياري: - ابحث عن متوسط جميع نقاط البيانات. ثم يتم قسمة مجموع جميع نقاط البيانات على العدد الإجمالي لنقاط البيانات لتحديد المتوسط.
- تحديد تباين كل نقطة بيانات. ثم يتم الحصول على التباين لكل منها عن طريق طرح المتوسط من القيمة لكل نقطة بيانات.
- تربيع تباين كل نقطة بيانات (الخطوة 2)
- مجموع قيم التباين حسب المربعات (الخطوة 3).
- عدد الملاحظات في مجموعة البيانات أقل من 1 يعادل مجموع قيم التباين التربيعية (الخطوة 4).
- تحديد الجذر التربيعي للحاصل (الخطوة 5).
الانحراف المعياري للبيانات المجمعة
عندما تكون هناك بيانات مجمعة أو توزيع تكراري مجمع، يمكن استخدام تردد قيم البيانات لحساب الانحراف المعياري. دعنا نأخذ مثالاً لفهم صيغة الانحراف المعياري للبيانات المجمعة بشكل أفضل:
مثال: بالنسبة للبيانات التالية، حدد المتوسط والتباين والانحراف المعياري:
حل : - ن = ∑ف = 55
- المتوسط = (∑fxi)/N = 925/55 = 16.818
- التباين = 1/(ن – 1)[∑fxi2 – 1/ن(∑fxi)2]
- = 1/(55 – 1) [27575 – (1/55) (925)2]
- = (1/54) [27575 – 15556.8182]
- = 222.559
- الانحراف المعياري = √التباين = √222.559 = 14.918
أفضل المدن التي تقدم فيها SPOTO دورة تدريبية للحصول على شهادة إدارة المشاريع عبر الإنترنت
الانحراف المعياري للبيانات غير المجمعة
بالنسبة لمجموعات البيانات المختلفة، يتم استخدام طرق مختلفة للانحراف المعياري. يقيس التشتت انحراف البيانات عن المتوسط أو موقع المتوسط. يمكن اكتشاف الانحراف المعياري باستخدام إحدى الطريقتين:
- طريقة المتوسط الفعلي
ستكون صيغة طريقة المتوسط الفعلي:
- σ = √(∑x−x̄)2 /n)
- الآن، دعونا نأخذ مثالاً لفهم أفضل لـ 3، 2، 5، و 6.
- كما ذكر أعلاه، باستخدام الصيغة لحساب المتوسط، سيتم حسابه على النحو التالي 16/4 = 4.
- الفروق التربيعية عن المتوسط الحسابي = (4-3)2+(2-4)2 +(5-4)2 +(6-4)2= 10
- وبالمثل، التباين = مربع الاختلافات من المتوسط / عدد نقاط البيانات = 10/4 = 2.5
- الآن، باستخدام الصيغة أعلاه، الانحراف المعياري = √2.5 = 1.58
- طريقة المتوسط المفترض
عندما تكون قيم x كبيرة، يتم تحديد المتوسط عن طريق اختيار قيمة عشوائية (A). ويطلق عليه أحيانًا أيضًا المتوسط المفترض بدلاً من القيمة العشوائية. يتم حساب الانحراف عن هذا المتوسط المفترض على النحو التالي d = x – A.
- σ = √[(∑(د)2 /ن) – (∑د/ن)2]
الانحراف المعياري للمتغيرات العشوائية
مقياس انتشار لتوزيع المتغيرات العشوائية الذي يحدد مدى انحراف القيم عن القيمة المتوقعة.
من الشائع كتابة أو X على أنه الانحراف المعياري للمتغير العشوائي X.
عند التعامل مع المتغيرات العشوائية المنفصلة، يتم تحديد الانحراف المعياري عن طريق إضافة مربع الفرق بين قيمة المتغير العشوائي والقيمة المتوقعة، والاحتمال التابع لقيمة المتغير غير المنتظم، مضروبًا في كل من قيم المتغير العشوائي، ثم أخذ الجذر التربيعي للمجموع. - المعادلة: σ=
- التباين، Var(X) = σ 2، يساوي مربع الانحراف المعياري.
مثال على الانحراف المعياري
الآن، دعونا نحسب الانحراف المعياري لعدد العملات الذهبية الموجودة على السفينة.
يوجد على متن السفينة 100 شخص. ووفقًا للإحصائيات، فإن عدد السكان 100 شخص. لذلك، إذا كنت تعرف العدد الإجمالي للعملات الذهبية التي يمتلكها كل شخص، فيمكنك استخدام معادلة الانحراف المعياري لعدد السكان الإجمالي.
لنأخذ عينة مكونة من 5 أشخاص كمثال ونطبق معادلة الانحراف المعياري على هذه المجموعة. مع حجم عينة يبلغ 5 أفراد، يمكنك استخدام معادلة الانحراف المعياري لحساب عينة من السكان.
افترض أن خمسة أشخاص لديهم عدد العملات الذهبية: 4، 2، 5، 8، و 6. - يقصد :
- x̄ = مجموع الملاحظات / العدد الإجمالي للملاحظات
- = 4+2+5+8+6 / 5
- = 5
الآن xn-x̄ لكل قيمة معطاة في مجموعة البيانات - 4-5 = -1
- 2-5 = -3
- 5-5 = 0
- 8-5 = 3
- 6-5 = 1
- ∑(x−x̄)2= (-1)2+ (-3)2+02+32+12
- = 20
الانحراف المعياري - σ = √[ ∑(x – x̄)2 / N ]
- = √20/4
- = √5
- = 2.236
- = 2.236
أطلق العنان لإمكاناتك مع أفضل شهادات Agile وطوّر مهاراتك الإدارية. تبنّى المرونة وكن قائدًا بثقة!
أمثلة على أسئلة امتحان شهادة PMP®
- كيف يتم حساب الانحراف المعياري لمجموعة من مدة مهام المشروع؟
احسب متوسط مدة المهام، ثم اطرح المتوسط من كل مدة للعثور على الانحرافات، ثم قم بتربيع هذه الانحرافات، ثم ابحث عن متوسط الانحرافات التربيعية، ثم خذ الجذر التربيعي لهذا المتوسط. - لماذا يعد الانحراف المعياري مهمًا في إدارة جدول المشروع؟
يساعد الانحراف المعياري على تحديد التباين في مدة المهام، مما يتيح لمديري المشاريع التنبؤ بالتأخيرات والتعديل للحفاظ على المشروع على المسار الصحيح. - بالنظر إلى أوقات إكمال مهام المشروع، كيف تفسر الانحراف المعياري المرتفع؟
يشير الانحراف المعياري المرتفع إلى وجود تباين كبير في أوقات إكمال المهام، مما يشير إلى المخاطر المحتملة والحاجة إلى مراقبة وتعديلات أكثر دقة. - كيف يساعد الانحراف المعياري في إدارة المخاطر بشكل أفضل على طول دورة حياة المشروع؟
يقوم الانحراف المعياري بقياس التباين، مما يسمح لمديري المشاريع بتقييم المخاطر بشكل أكثر دقة وتنفيذ استراتيجيات التخفيف المناسبة. - كيف يمكن تطبيق الانحراف المعياري على ميزانيات المشاريع لتحقيق دقة أفضل في الميزانية؟
من خلال تحليل فروق التكلفة، يساعد الانحراف المعياري مديري المشاريع على تقدير الميزانيات بشكل أكثر دقة، مع مراعاة التقلبات المحتملة وتقليل مخاطر تجاوز الميزانية.
خاتمة
تغطي المقالة أعلاه معظم المواضيع التي تتعلق بشكل مباشر بالانحراف المعياري، والانحراف المعياري المتوسط، وغير ذلك الكثير. نظرًا لوجود العديد من الأشياء الأساسية مثل البيانات المستمرة أو المنفصلة وما إلى ذلك، فإن المقالة لا تغطي بعض المصطلحات الواضحة، مثل متوسط التباين وغيره. الانحراف المعياري ليس شيئًا صغيرًا. إنه مجرد جزء صغير من مفهوم كبير جدًا.
غالبًا ما يحصل طلاب الهندسة وعلوم الكمبيوتر على هذا الفصل في مناهجهم الدراسية. أيها الطلاب، لا تترددوا في طرح أي أسئلة في التعليقات. تعد وظيفة محلل البيانات واحدة من المهن الشائعة التي يمكن لأي شخص القيام بها من خلال إتقان مفهوم الانحراف المعياري والموضوعات الأخرى ذات الصلة. يمكنك دائمًا الالتحاق بدورة تدريبية SPOTO PMP لفهم الإحصاءات بشكل أفضل وتنفيذها في الحياة الواقعية.
الأسئلة الشائعة - ماذا يعني الانحراف المعياري 1؟
الانحراف المعياري هو مقياس إحصائي للتباين في مجموعة سكانية أو مجموعة. يشير الانحراف المعياري بمقدار واحد إلى أن 68% من السكان يقعون ضمن الانحراف المعياري عن المتوسط، زائد أو ناقص. على سبيل المثال، افترض أن متوسط طول الذكور هو 5 أقدام و9 بوصات، والتباين المعياري هو ثلاث بوصات. إذن، 68% من جميع الذكور يتراوح طولهم بين 5 أقدام و6 بوصات و6 أقدام، 5 أقدام و9 بوصات زائد أو ناقص 3 بوصات. - ما هو الانحراف المعياري الجيد؟
عند النظر إلى التمثيل البياني، تعتبر مجموعة البيانات القريبة من المتوسط جيدة. وعند النظر إلى حساب الانحراف المعياري فقط، يعتبر معامل التباين أو CV الذي تعتمد قيمته على CV < 1 انحرافًا معياريًا جيدًا. - كيف تعرف إذا كان الانحراف المعياري مرتفعًا أم منخفضًا؟
إن إحدى أسهل الطرق لتحديد ما إذا كان الانحراف المعياري مرتفعًا أم منخفضًا هي من خلال التمثيل البياني. وكما ذكرنا أعلاه، فإن حساب الانحراف المعياري ليس بالصعوبة التي يتصورها الناس. كما أن تصوير الانحراف المعياري من خلال الرسم البياني أسهل ويساعد الشخص على تحديد ما إذا كان الانحراف المعياري مرتفعًا أم منخفضًا. بشكل عام، إذا كان معامل التباين أو CV >= 1، فهو مرتفع؛ وإلا فهو منخفض. يتم حساب معامل التباين على أنه الانحراف المعياري مقسومًا على المتوسط. - ما هو التباين القياسي في إدارة المشاريع؟
في إدارة المشاريع، يشير التباين المعياري إلى الانحراف المتوقع عن مقاييس الأداء المخطط لها، مثل التكلفة أو الجدول الزمني. ويُستخدم لتقييم ومراقبة التباين في أداء المشروع.
